简介
本文将要讨论这一课题的主要概念,诸如深度学习以及无复杂layman形式运算的深度网络。
真实数据的实验,通过定量和比较(无法定量和比较),证实(或证伪)深度神经网络的理论优势。当前的任务是分类。我们要基于深度神经网络模型创建一个指标和一个EA,根据客户端/服务器的方式进行运作,并对它们进行测试。
本文的读者应该对神经网络中使用的基本概念已有一定程度的了解。
1. 第二代神经网络
神经网络设计用于解决图像处理领域的广泛问题。
下面是典型的神经网络能够解决的问题列表:
- 函数逼近的一组点(回归);
- 根据指定类集进行数据分类;
- 识别预先未知的原型类的数据聚类;
- 信息压缩;
- 恢复丢失的数据;
- 联想记忆;
- 优化,最优控制等。
不在上述列表中的本文仅将讨论“分类”。
1.1. 连结的体系结构
信息处理的方式很大程度上受到网络中反馈回路的有误。如果神经元之间没有反馈链路(例如,该网络具有一个顺序层级结构,每个神经元只接收来自前一层的信息),网络中的信息处理是单向的。一个输入信号经由一系列神经网络层处理,并被同层级数量相等的触点所接收。
反馈回路的存在会使得神经网络的动态(此处称为循环)不可预测。事实上,网络可能“死循环”并且永远无法给出响应。与此同时,根据图灵的结论,对于任意循环网络没有算法能够确定它的元素是否会进入平衡状态(停机问题)。
一般来说,基于在循环网络中的神经元参与处理信息许多次的事实,允许这类网络以不同的方式在更深的层级上进行信息处理。在这种情况下,需要采用特殊的措施以免网络陷入死循环。例如,使用对称节点,像Hopfield网络或者强制限制迭代的次数。
|
训练类型 节点类型 |
有“监督的” | 无“监督的” |
|---|---|---|
| 无反馈环 |
多层传感器(函数逼近,分类) |
竞争性网络,自组织图(数据压缩,特征分离) |
| 有反馈环 |
循环传感器(时间序列预测,在线训练) |
Hopfield网络(相联存贮器,数据聚类,优化) |
表 1. 按连接和培训类型分类的神经网络
1.2. 神经网络的主要类型
从神经元开始,神经网络走过了很长的发展道路。今天大量不同的结构和训练模式的神经网络被使用。
最著名的有:
1.2.1. 多层全连接的前馈网络MLP(多层感知器)
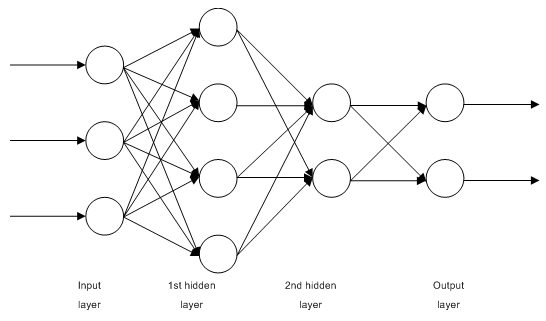
图 1. 多层神经网络结构
1.2.2. Jordan网络是典型的循环网络并且和Elman网络类似。
它可以被看成是在输入层带有额外承接层神经元的反馈网络。
这些承接层神经元从输入层神经元中自反馈(直接反馈)。承接层神经元保存网络的当前状态。再Jordan网络中,承接层神经元的数量和输入层神经元的数量必须一致。
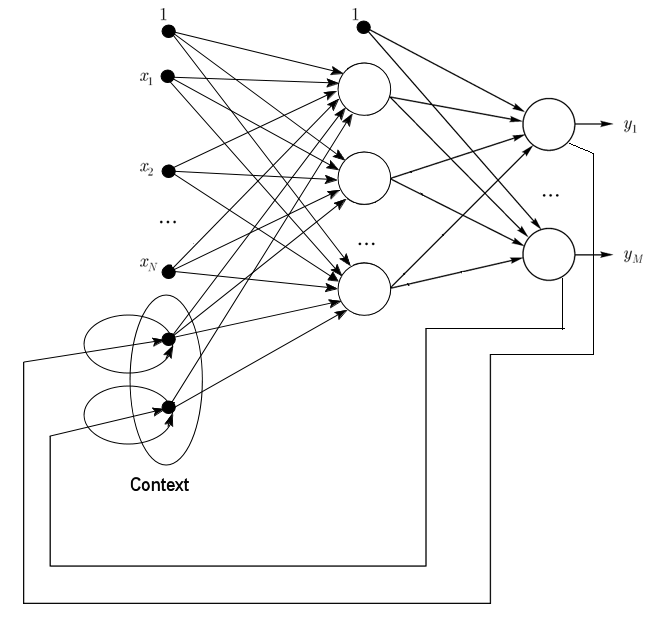
图 2. Jordan网络结构
1.2.3. Elman网络是典型的循环网络并且和Jordan网络类似。Elman和Jordan网络的区别在于在Elman网络中承接层神经元的输入由输出神经元而不是隐含神经元决定。另外,在承接层神经元中无直接反馈。
在一个Elman网络中,承接和隐含神经元的数量必须一致。Elman网络的主要优点在于承接层的神经元数量不像Jordan网络那样由输出层决定,而是由隐含层神经元的数量决定的,这就使得网络更具弹性。隐含神经元不像输出神经元那样,它们能够方便的被添加或者移除。
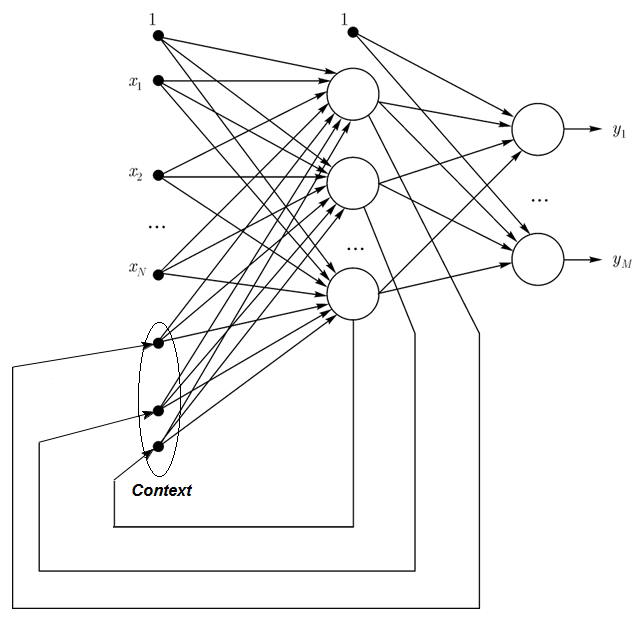
图 3. Elman网络结构
1.2.4. 径向基函数网络(RBF)- 是一个前馈神经网络,包含径向对称神经元的一个中间(隐藏)层。这样的神经元通过某些非线性Gaussian算法将其同特定输入向量间的距离转换为中心距。
RBF网络相比多层前馈网络而言有很多优点。首先,它们模仿(不确定这个词是否恰当)仅有一个中间层的任意一个非线性函数,省得开发者决定层数。然后,输出层线性组合参数就能够使用众多广为人知的线性优化算法来进行优化了。后者运行很快并且没有会极大干扰反向传播的本地极小值。这也是为何当使用反向传播时RBF网络的学习速度要块很多的原因。
RBF的缺点:这些网络具有弱外推特性并且当输入向量非常大时会变的低效。
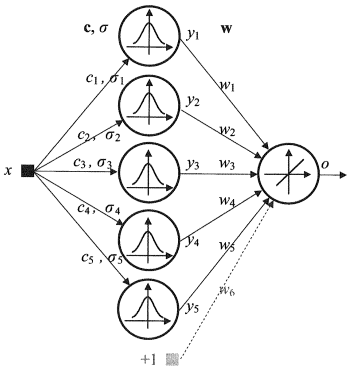
图 4. RBF的结构
1.2.5. 动态学习矢量量化,DLVQ 网络同自组织图(SOM)非常类似。不像SOM,DLVO能够进行有监督的学习并且和原型之间没有依赖关系。矢量量化比聚类的用途更为广泛。
1.2.6. Hopfield网络在执行过程中,这种网络动态收敛到平衡状态中的一种。这些平衡状态是称为网络能量的本地功能极小值。这样的网络可以用作一个内容寻址关联存储器系统、一个过滤器以及解决一些优化问题。
和许多神经网络运行直到接收到特定数量的反馈不同的是,Hopfield网络运行直到达到平衡状态,即网络的下一个状态和前一个状态完全一样。在这种情况下初始状态是一个输入模式,在平衡状态下接收输出图像。训练Hopfield网络需要同时再输入和输出层给出训练模式。
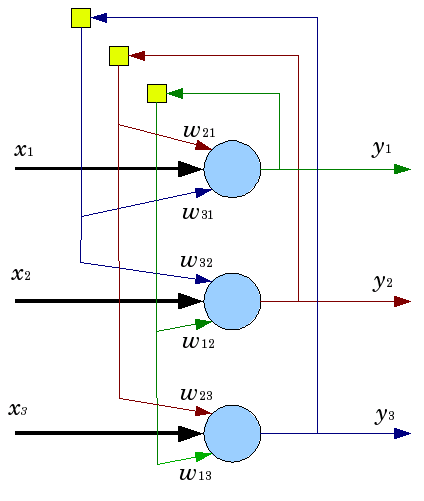
图. 5. 三个神经元的Hopfield网络结构
尽管有吸引人的特性,经典的Hopfield网络还远远谈不上完美。它内存有限仅占网络N中大约15%的神经元,然而内存直接寻址系统能够使用N比特储多达2N个不同的图像。
另外,Hopfield网络无法识别图像,如果该图像相对于它的初始储存的位置被移位或转动。这样或那样的缺陷使得Hopfield网络更多的用于理论模型研究而非日常实用的工具。
其他很多(Hemming循环网络,Grossberg网络,自适应共振理论网络(ART-1, ART-2)等)未在本文中提及,因为它们超过了我们的兴趣范围。
1.3. 训练方法
能够学习新的事物是人类大脑主要的功能。对于人工神经网络而言,学习是构建网络结构(神经元之间的连结结构)以及触突权重(信号的影响系数),以便能够获得解决实际问题的有效方法。通常在一个数据样本上来训练神经网络。训练是一个特定算法的执行过程,随着训练的进行网络对输入信号的响应结果应该逐渐改善。
有三个主要的学习模式: 有监督的, 无监督的以及混合的。第一种情况下,每个输入的正确结果都是已知的并且网络权重用于最小化误差。无监督学习用于样本分类,阐释数据的内在结构和特性。混合模式下以上两种方式都使用。
1.3.1. 神经网络学习的主要规则
与之相关的网络构建算法主要有四种:误差纠正,Boltzmann法则,Hebb法则和竞争性算法。
1.3.1.1. 误差纠正
每一个输入样本都有一个特定的期望输出值(目标值),可能和实际(预测)值不符。误差纠正学习算法用目标和预测值之间的误差作为权重调整的直接依据来缩小误差。只有当出现误差时训练才被执行。这种学习方法有许多优化版本。
1.3.1.2. Boltzmann 规则
Boltzmann法则是一种混沌学习算法,它类比热力学理论中的原则。它根据期望的概率分布来调整神经元权重系数。Boltzmann学习算法可以被认为是误差纠正算法的一个特例,它的误差是指两个模型中状态之间的相关性差异。
1.3.1.3. Hebb 规则
Hebb算法是最著名的神经网络学习算法。这个算法的思想是,如果一个突触的两侧的神经元同时并定期时常激活,那么触突连结的强度增加。此处一个重要的特性是,触突的权重仅当其连结的神经元激活时才改变。有很多此算法的变种,区别在于触突权重修改的方式。
1.3.1.4. 竞争性学习
和Hebb学习算法不同的是,众多的输出神经元可以同时被激活,并且相互之间存在竞争关系。权值累计最大的输出神经元“获胜”并且“赢家通吃”。其他输出神经元的输出置为非激活状态。当进行学习时,只有“赢家”的权重值得到修正,使之逐渐逼近当前输入实例。
为了解决不同的问题,对应有许多种学习算法。反向传播算法就是其中最有效的现代算法之一。其背后的原理是触突权重的改变发生在误差函数的局部梯度附近。
实际值和网络输出层的正确响应值之间的差异是会反向传播的 - 沿着信号流方向(图.5)。这样每个神经元都可以定义属于它的网络累计误差的权重分布。最简单的学习规则是最速下降法,也就是触突的权值根据它们的累计误差分布按比例改变。
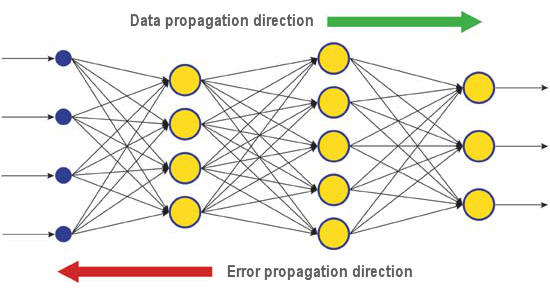
图. 6. 当通过反向传播进行学习时的数据和误差扩散模式
当然,这个类型的神经网络学习不能保证最佳的学习结果,因为总有一定的概率算法陷入局部极小值。有特殊的技巧能够识别找到的结果是否局部极点。如果当使用多次此技术后,神经网络的决策都是一致的,那么能够得出结论这个结果很可能就是最优结果。
1.4. 缺点
- 利用神经网络的主要困难是所谓的“维数灾难”。当输入维度及层数增加后,网络的复杂度和学习时间将呈指数级增长并且接收到的结果并非总是最优的。
- 使用神经网络的另一个困难在于传统的神经网络无法解释它们如何解决问题。在某些医药应用领域对此的解释比结果本身更重要。除了最简单的我们不感兴趣的情况外,内部结果表示是机器复杂的,几乎是不可能进行分析的。
2. 深度学习
由于深度学习算法的成功实施,今天以第三代神经网络为代表的机器学习理论和实践正在经历一场“深刻的革命”。和上世纪八九十年代经典的第二代神经网络不同,新的学习模式解决了许多问题,突破了限制并且成功应用到传统的神经网络中。
经过深度学习算法训练的神经网络并不是简单的比其他方法精度高,而是在某些情况下能揭示对输入信息的理解雏形。图像识别和文本信息分析是最好的例子。
今天,最先进的工业计算机视觉和语音识别方法是基于深度神经网络的。IT业巨头ru Aple,Google,Facebook正雇佣研究者开发深度神经网络。
2.1. 背景
一组由Geoffrey E. Hinton教授领导的多伦多大学研究生,在一次由Merk赞助的竞赛中获得了第一名。使用有限的数据集,描述15个分子的化学结构,G. Hinton的团队创建并应用一种特殊的程序系统来确定哪一个分子最有可能是有效的药物。
这项工作的特殊之处在于,开发者使用基于深度学习的人工神经网络来完成。正由于此那个系统基于非常有限的源数据计算并得出结果,而通常训练一个神经网络需要输入大量的信息。
Hinton'团队的成果令人印象深刻,因为团队在最后时刻才参加比赛。不仅如此,深度学习系统的开发无需与其相关的特定分子领域的知识。深度学习的成功应用是人工智能领域2012年的又一重大成就。
因此在2012年,来自Google的Jeff Dean 和 Andrew Y. Ng呈现了一个新的图像识别系统,精确度达15.8%,他们使用ImageNet网络中20,000个不同对象的140万副图片来训练一个包含16,000个节点的集群系统。去年在一项由瑞士科学家创建的识别交通信号图片的项目中,神经网络系统超越了人脑。获胜的程序准确地从50,000张图片集中分辨出了99.46%的图片;在一组32个参与者中最好的成绩是99.22%,人脑平均成绩是98.84%。在2012十月,微软科学计划成员Richard F. Rashid参加了在中国天津举办的一个会议,会上展示了一项技术,模拟其声音同步将英语翻译成中文。
所有这些技术展现了深度学习方法在人工智能领域取得的一定程度的突破。深度学习理论的主要贡献来自于Hinton教授,他是英国科学家George Boole的玄孙,。
深度学习理论在多个展现层上将普通机器学习方法和分析输入信号的特殊算法相结合。新方法即深度学习算法的特点是,算法直到找到足够多的、能够影响问题中所涉对象参数的信息展现层,才开始进行学习。
这样,基于此方法的神经网络相比传统神经网络来说需要更少的输入数据来做学习,并且一个接受过训练的网络能够更加精确的进行信息分析。Hinton教授和他的团队声称他们的技术尤其是在处理 多维度、结构良好的信息阵列时表现更佳。
人工智能技术(AI),尤其是深度学习技术被广泛的使用在不同的系统中,包括基于Nuance Communications技术的Apple Siri智能个人助手以及Google街景的地址识别系统。然而,科学家们评估这个领域内的成功非常小心,因为在创建人工智能系统的历史中充满了希望与失望。
在60年代,科学家相信只需要再过10年就能够创造出一个完美的人工智能系统来。接着,在这个领域“冰河期”过后的80年代,一股年轻公司提供“现成人工智能系统”的热潮出现了,一直持续到现在。如今借助云服务所能提供的强大计算能力,为使用新理论和算法的神经网络的实现提供了可能。
值得注意的是甚至像卷积神经网络、Boltzmann机这类第三代神经网络除了名称外,同生物神经没有一点相似之处。
新学习算法分两步实现:第一步,有关输入数据的内部结构信息通过逐层的无监督训练,从一个未格式化的大数组中被提取出来。然后,在一个多层神经网络中使用这些信息,将格式化后的数据用现有算法进行有监督训练。与此同时,未格式化的数据必须尽可能的多。格式化后的数据可以相对较少。在我们的场景中这不是最重要的。
2.2. 自动编码器自动编码器和受限玻尔兹曼机。差异与特点
2.2.1. 自动编码器
第一个自动感应器是福岛神经认知机。
其结构如图7所示。

图. 7. 福岛神经认知机
自动感应器(AA)的目的是在输出端接收到尽可能精确的输入数据的镜像。
有两种类型的AA — 生产与合成。受限波尔兹曼机属于第一类,自动编码器代表了第二种类型。
一个自动编码器是一个只有一个开放层的神经网络。使用无监督学习算法和反向传播算法,它将目标值设置成和输入向量相同,如:y = x。
图8是一个自动编码器的例子。
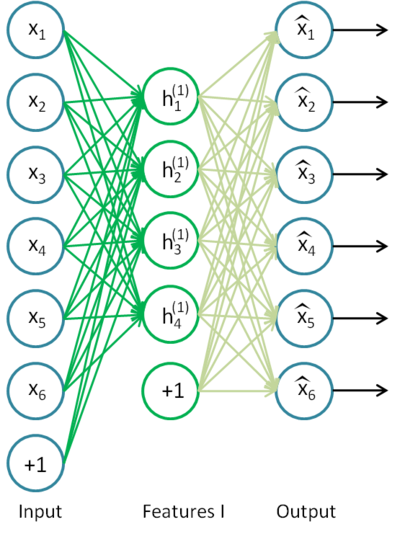
图. 8. 自动编码器结构
自动编码器尝试构建函数h(x)=x。换句话说它试图找到一个逼近函数确来保神经网络的反馈约等于输入参数。为了使问题的解决方案一般化,开放层的神经元数量必须比输入数据的维度的少(如图所示)。
当输入信号传递到网络的输出层数据会被压缩。例如,如果输入向量是一个10x10像素(100个特征值)的图片灰度值,隐含层的神经元数量为50,那么网络被迫学习进行图像压缩。h(x)=x意味着基于隐含层50个激活神经元,输出层要将初始图像复原成100个像素。这样的压缩是可行的,如果有隐含节点,特征相关性或者任何关联结构。这样一个自动编码器能在此意义上提醒主成分分析方法(PCA)输入数据被压缩了。
令人惊喜的是,Bengio等人进行了这个实验,(2007)。实验显示在随机梯度下降训练时,隐含神经元数量大于输入数据数量(也称为“过剩”)的非线性自动编码网络在对网络的输入一致性误差的表达方面有益。
接着,当稀疏的思想出现时,稀疏模式自动编码器被广泛的使用开来。
稀疏自动编码器是隐含神经元数量显著多余输入数据维度的自动编码器,但是它们具有稀疏激活模式。所谓稀疏激活模式是指,隐含层中激活神经元的数量远小于非激活神经元的数量。通俗的说就是当神经元激活时它的函数值接近于1。如果使用一个sigmoid函数,那么非激活的神经元的值必须约等于0(对于双曲正切函数来说其值必须接近-1)。
这是自动编码器的一个变种,称为降噪自动编码器(Vincent等人,2008)。它和自动编码器一样但是训练方式有些特别。当训练这个网络时,“损坏”的数据是输入(用0代替)。与此同时,同输出数据相比有在“正确”的数据。这样自动编码器能够恢复受损数据。
2.2.2. 受限玻尔兹曼机,RBM。
我们不打算聚焦在受限玻尔兹曼机(RBM)的历史上。我们所知道的是带有反馈的循环网络非常难以训练。正因为学习困难,受限的循环模型出现了,使得学习算法变得简单,能够被应用到实际中。Hopfield神经网络就是这类模型之一。John Hopfield引入了网络能量概念,将神经网络的动态与热力学中的概念作比较。
在通往RBM路上的下一站是规则玻尔兹曼机。它们和Hopfield网络不同之处在于具有随机特性,并且它的神经元被分为可见的和隐藏的两组(类似隐马尔科夫模型)。受限波尔兹曼机和规则波尔兹曼机的不同之处在于同层神经元间没有关联。
图9表示了一个RBM结构。
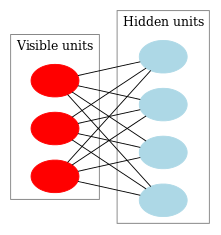
图. 9. 一个RBM结构
这个模型的特别之处在于,在一组神经元当前状态下,其他组神经元的状态都是相互独立的。现在我们可以来看看这个特性发挥重要作用的其它理论。
解读和观点
一个RBM可以理解成和隐马尔科夫模型类似。我们能观察到一些(可见神经元)的状态,一些隐含状态我们无法直接见到(隐藏神经元)。我们能够得到依赖可观测状态的隐藏状态的概率统计结果。模型一经训练完毕,我们就有机会得出结论,即从可见状态中可知隐藏状态遵循贝叶斯准则。这就允许通过概率分布来产生数据用于训练模型。
这样我们就能够制定训练模型的目标:模型参数将被调整,使得从初始状态重构的向量和原始值最接近。一个重构向量是隐含状态的概率推演的产物,隐含状态则是可见状态的概率推演产物,例如原始向量。
训练算法是对比差分法CD-k。
这个算法由Hinton教授在2002年发明,它异常简单。主要思想是将数学期望值用自定义值取代。介绍Gibbs采样思想。
CD-k看上去是这样的:
- 可见神经元的状态被设置为同输入模式一致;
- 绘制隐含层状态的概率分布;
- 隐含层的每个神经元被分配状态“1”,意味着同当前状态的分布一致。
- 可见层状态的概率分布基于隐含层绘制。
- 如果当前迭代次数少于k,那么返回第二步;
- 绘制隐含层状态的概率分布;
在Hinton的报告中是这样的:
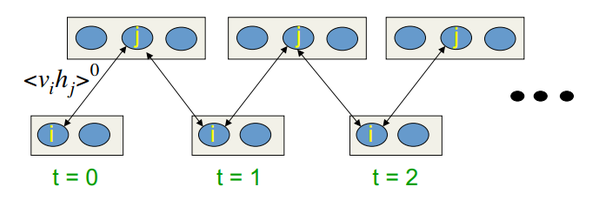
图.10. CD-k学习算法
换句话说,我们采样时间越长,梯度越精确。Hinton教授声称从只进行一次采样迭代的CD-1算法获得的结果就已经不错了。
2.3. 堆栈式的自动连结网络。堆栈式自动编码器 SAE, 堆栈式自动编码器(堆栈 RBM)
为了解析输入数据集更高层级的抽象信息,自动关联器被加到网络中。
图11表示一个堆自动编码器的结构和一个神经网络,两者一起组成了一个权重由堆自动编码器初始化的深度神经网络。
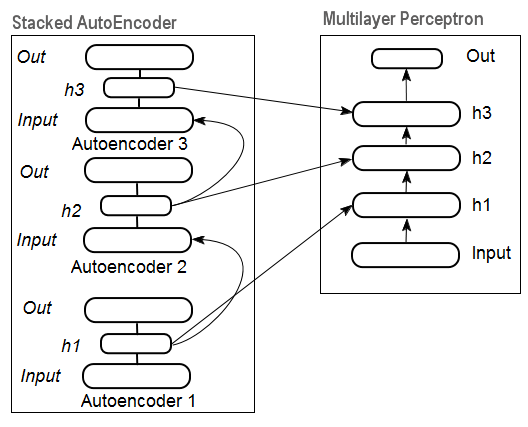
图. 11. DN SAE结构
图12是一个堆RBM(SRBM)模式以及一个神经网络,两者共同组成了一个权重由SRBM初始化的深度神经网络。
这些深度神经网络结构的例子都强调了信息从下至上被解析这一事实。
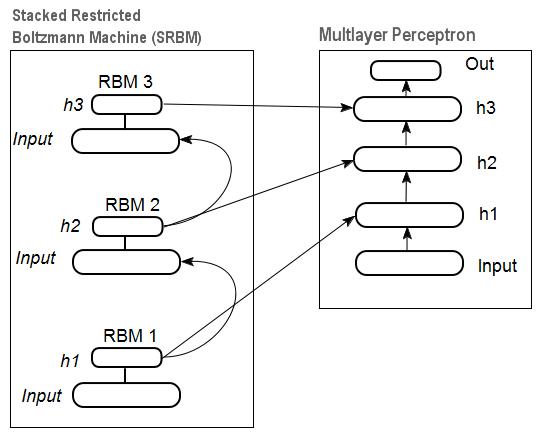
图. 12. DN SRBM结构
2.4. 深度网络训练(DN)。阶段。特点
深度神经网络的训练由两个步骤组成。首先,一个自动关联器网络(SAE或者SRBM,取决于DN类型)用未格式化的数据阵列进行无监督训练。之后,普通MLP的隐含层神经元由训练后接收到的隐含层权重初始化。图11和图12表示一个训练模式和传输过程。在第一个AE/RBM训练之后,隐含层神经元的权重成为第二个的输入,以此类推。通过这种方式,结构体的一般信息(线,周线,模式等)从数据中解析出来。
第二步就是对MLP(有监督训练)使用众所周知的方法在格式化后的数据集上进行微调了。试验证明这种初始化方法能将MLP的隐含层神经元权重设置为全局最小值,并且后续的微调耗时非常短。
进一步,对于超过三层的深度神经网络,Hinton教授建议微调应分两步走。首先仅训练前两层,然后再训练网络的其余层。
需要注意的是一个SRBM相对于SAE来说,无监督训练结果的稳定性低一些。
注意 这些概念经常被搞混。一个SRBM由 深度信任网络DBN确定。虽然RBM从DBN派生而来,但它们是的结构完全不同。一个DBN是一个多层神经网络,其隐含层神经元的权值由二进制模式随机初始化。
3. 实际实验
用R语言实现的深度神经网络。
3.1. R语言
历史。R语言是一种程序语言,是一个用于统计计算和制图的环境,由新西兰科学家Ross Ihaka和Robert Gentleman 1996年在奥克兰大学发明。
R是一个GNU开源软件项目,他们基本原则由如下几条:
- 有执行任何目的程序的自由(自由0);
- 有学习程序如何运行记忆将其修改为己所用的自由(自由1);
- 有分发程序的副本帮助其他人的自由(自由2);
- 有改进程序使社会从其改进中收益的自由。
从历史的角度看,R是S的替代物,后者是由John Chambers和其同事1976年在贝尔实验室发明的。今天,R仍旧由包含John Chambers在内的核心开发小组不断优化中。
为了重现实验,你必须安装R和Rstudio。在何处下载以及如何下载的相关信息,你可以在互联网上找到。如果由任何问题,我们可以在本文的评论部分探讨。
R的优点:
- 如今R在统计计算领域是标准。
- 它正被全球大学的科研团队开发和支撑中。
- 有大量的数据挖掘一切先进领域的开发包。一个想法的公开和用R开发包实现之间的时间间隔通常不会超过2周。
- 最重要的是,它是完全免费的。一位开源操作系统的著名开发者曾说过:“程序就像性一样 — 最好是免费的”。
3.2. 实现方案和问题
有两个实现方式。
第一个是使用John Hinton独特的Matlab程序。这就需要“R.matlab”。这个包中有writeMat() 和 readMat() 方法,用来读写MAT文件。它能够同本地加载的或远程服务端运行的Matlab v6及更高版本之间进行通信(编码、发送接收对象等)。详情见开发包描述。这是对于习惯使用Matlab的人的方法。我没有尝试过使用这个方法,但将Matlab和MQL建立连接是有可能的。
第二种实现方式是使用R开发包。我们将深入研究这个方法。
据我所知有三个开发包和本文的主题有关。
-
"deepnet"是一个实现DN SAE和DN SRBM模型的简单开发包。有监督和无监督学习的输入数据集长度是一样的。这使得分两步实施系统微调的可能性不存在了。一开始就要用于构建和测试模型。
-
"darh" 是一个先进、涵盖面广的DN SRBM模型开发包。其中有一个DN SAE模型但是我没有加载成功。这个包是给经验丰富的用户准备的,它能够创建和调整任意复杂度的模型。它基于Hinton独特的Matlab语言程序。
-
"H2O"是一个用于在巨大数据集上(csv文件格式)训练深度网络(不仅仅是)的广泛开发包。
下面的实验我们将使用“deepnet”包。
3.3. 准备用于试验的输入和目标数据
如今数据挖掘有一个特定的执行顺序:
- 选择输入数据(研究、分析、预处理、评估);将数据集分为训练集、效验集和测试集(抽样);
- 在训练集上得到模型,在效验集上验证;
- 用测试样本评估模型质量,确定最佳模型参数或者通过特定的手段获得匹配测试集的最佳模型。
- 模型开始工作。
第一步最费时间并且对最终结果的产生最重要。老实说,这一步没有规则可循并且一般来说几乎是一种艺术。绝大多数情况下取决于研究者的经验。然而!为了选择最重要的输入数据集,对其进行量化评估是非常重要的。为一个特定模型自动选择最佳参数在这种情况下甚至更好。R语言提供了广泛的功能,能够解决所有实现中的挑战。
源数据不仅重要,而且有许多方面需要考虑。它可以单独另起一篇文章讨论。由于本文的目标是将复杂的事情用简单的语言表述出来,我们将重点讨论关键点而不会过多纠缠于细节。
3.3.1. 源数据
要进行分类我们需要一组独立的(输入)变量以及一个目标变量。既然深度学习网络的优势在于能够在大量的输入采样数据上快速地进行学习,让我们创建一个含有17个预测因子(11个指标)的输入数据集。ZigZag充当目标变量。在R中下载4000个柱形的开盘、最高、最低和收盘价向量。下载方法在下文指标编写中讨论。在这步中它还不重要。所有进一步的计算都将在R中实现。
由4个向量构建一个矩阵,平均价格和柱体大小。将其转换成一个函数:
pr.OHLC <- function (o, h, l, c)
{
#Unite quote vectors into a matrix having previously expanded them
#Indexing of time series of vectors in R starts with 1.
#Direction of indexing is from old to new ones.
price <- cbind(Open = rev(o), High = rev(h), Low = rev(l), Close = rev(c))
Med <- (price[, 2] + price[, 3])/2
CO <- price[, 4] - price[, 1]
#add Med and CO to the matrix
price <- cbind(price, Med, CO)
}
查看结果(08.10. 14 12:00 时的状态)
> head(price)
Open High Low Close Med CO
[1,] 1.33848 1.33851 1.33824 1.33844 1.338375 -4e-05
[2,] 1.33843 1.33868 1.33842 1.33851 1.338550 8e-05
[3,] 1.33849 1.33862 1.33846 1.33859 1.338540 1e-04
[4,] 1.33858 1.33861 1.33856 1.33859 1.338585 1e-05
[5,] 1.33862 1.33868 1.33855 1.33855 1.338615 -7e-05
[6,] 1.33853 1.33856 1.33846 1.33855 1.338510 2e-05
3.3.2. 输入数据(预测器)
指标列表。指标是随机选择的,并没有特意要获得输入的最大差值。
所有指标的计算都使用包含众多指标的“TTR”包。
3.3.2.1. Welles Wilder的运动方向指数 - ADX(HLC, n) - 4个输出 (Dip, Din,DX, ADX)
观察其在开始的200个柱形上计算后的样子:
> library(TTR) > adx<-ADX(price, n = 16) > plot.ts(head(adx, 200))
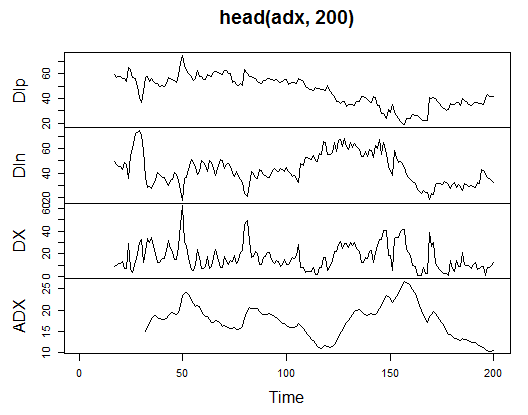
图.13. Welles Wilder方向运动指数指标 - ADX(HLC, n)
> summary(adx) DIp DIn DX ADX Min. :15.90 Min. : 5.468 Min. : 0.00831 Min. : 5.482 1st Qu.:41.21 1st Qu.: 33.599 1st Qu.: 8.05849 1st Qu.:14.046 Median :47.36 Median : 43.216 Median :16.95423 Median :18.099 Mean :47.14 Mean : 46.170 Mean :19.73032 Mean :19.609 3rd Qu.:53.31 3rd Qu.: 55.315 3rd Qu.:27.97471 3rd Qu.:23.961 Max. :80.12 Max. :199.251 Max. :81.08751 Max. :52.413 NA's :16 NA's :16 NA's :16 NA's :31
在矩阵开始处有31个未定义值(NA)。然后对所有指标进行相同的运算,此处未详细解释。
3.3.2.2. aroon(HL, n) - 1个输出(振荡器)
计算并观察只有一个变量的“振荡器”指标的初始200个柱形。
> ar<-aroon(price[ , c('High', 'Low')], n = 16)[ ,'oscillator']
> plot(head(ar, 200), t = "l")
> abline(h = 0)
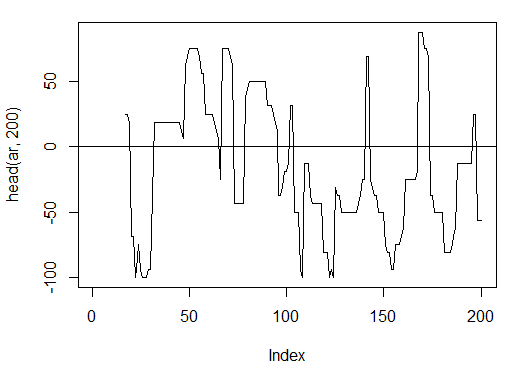
图. 14. 指标 aroon(HL, n)
> summary(ar) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -100.00 -56.25 -18.75 -7.67 43.75 100.00 16
3.3.2.3. 商品通道指数 - CCI(HLC, n) - 1个输出
> cci<-CCI(price[ ,2:4], n = 16) > plot.ts(head(cci, 200)) > abline(h = 0)
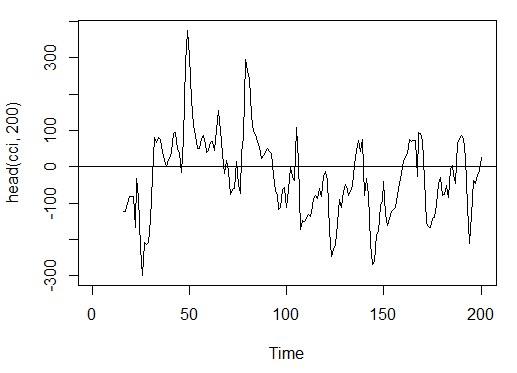
图. 15. 商品通道指数指标 - CCI(HLC, n)
> summary(cci) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -469.10 -90.95 -18.74 -14.03 66.91 388.20 15
3.3.2.4. Chaikin 波动率 - chaikinVolatility (HLC, n) - 1个输出
> chv<-chaikinVolatility(price[ , 2:4], n = 16) > summary(chv) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.67570 -0.29940 0.02085 0.12890 0.41580 5.15700 31 > plot(head(chv, 200), t = "l") > abline(h = 0)
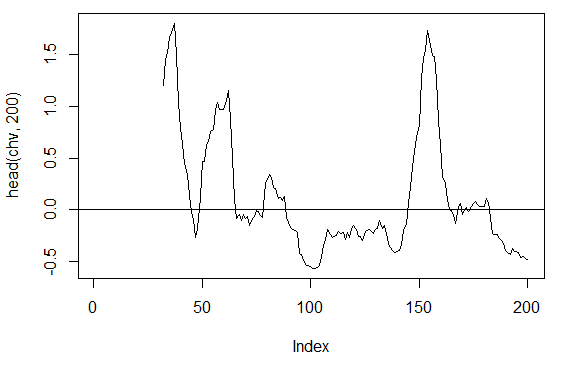
图. 16. 指标 chaikinVolatility (HLC, n)
3.3.2.5. Chande 动量振荡器 - CMO(Med, n) - 1 out
> cmo<-CMO(price[ ,'Med'], n = 16) > plot(head(cmo, 200), t = "l") > abline(h = 0)
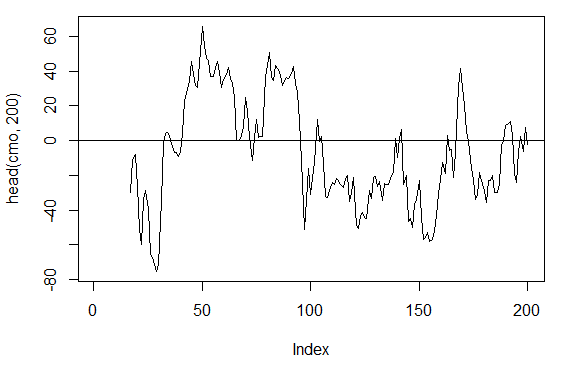
图. 17. Chande 动量振荡器指标 - CMO(Med, n)
> summary(cmo) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -97.670 -32.650 -5.400 -6.075 19.530 93.080 16
3.3.2.6. MACD 振荡器 - MACD(Med, nFast, nSlow, nSig) 使用1个输出(macd)
> macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'] > plot(head(macd, 200), t = "l") > abline(h = 0)
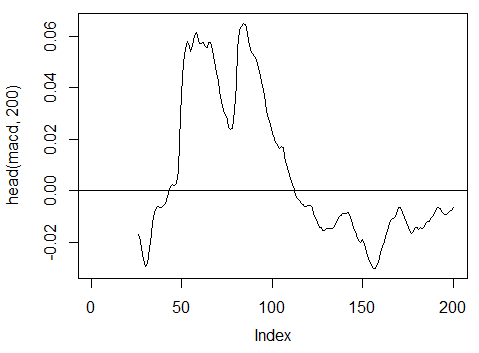
图. 18. MACD 振荡器指标
> summary(macd) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.346900 -0.025150 -0.005716 -0.011370 0.013790 0.088880 25
3.3.2.7. OsMA(Med,nFast, nSlow, nSig) – 1 out
> osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'] > plot(head(osma, 200), t = "l") > abline(h = 0)
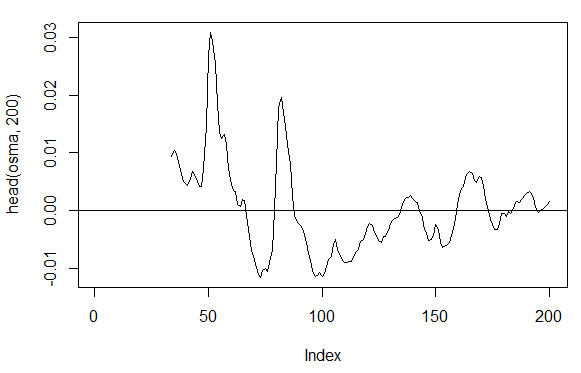
图. 19. 指标 OsMA(Med,nFast, nSlow, nSig)
> summary(osma) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.10560 -0.00526 0.00034 0.00007 0.00646 0.05922 33
3.3.2.8. 相对强弱指数 - RSI(Med,n) – 1个输出
> rsi<-RSI(price[ ,'Med'], n = 16) > plot(head(rsi, 200), t = "l") > abline(h = 50)

图. 20. 相对强弱指数指标 - RSI(Med,n)
> summary(rsi) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 5.32 37.33 47.15 46.53 55.71 84.82 16
3.3.2.9. 随机振荡器 - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3) - 3个输出
> stoh<-stoch(price[ ,2:4], 14, 3, 3) > plot.ts(head(stoh, 200))
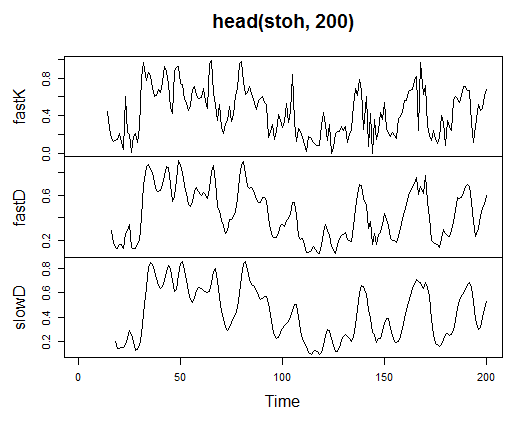
图. 21. 随机振荡器指标 - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
> summary(stoh) fastK fastD slowD Min. :0.0000 Min. :0.01782 Min. :0.02388 1st Qu.:0.2250 1st Qu.:0.23948 1st Qu.:0.24873 Median :0.4450 Median :0.44205 Median :0.44113 Mean :0.4622 Mean :0.46212 Mean :0.46207 3rd Qu.:0.6842 3rd Qu.:0.67088 3rd Qu.:0.66709 Max. :1.0000 Max. :0.99074 Max. :0.97626 NA's :13 NA's :15 NA's :17
3.3.2.10. 随机动量指数 - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9) — 2个输出
> smi<-SMI(price[ ,2:4],n = 13, nFast = 2, nSlow = 25, nSig = 9) > plot.ts(head(smi, 200))

图. 22. 随机动量指数指标 - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
> summary(smi) SMI signal Min. :-82.185 Min. :-78.470 1st Qu.:-33.392 1st Qu.:-31.307 Median : -9.320 Median : -8.839 Mean : -8.942 Mean : -8.985 3rd Qu.: 15.664 3rd Qu.: 14.069 Max. : 71.878 Max. : 63.865 NA's :25 NA's :33
3.3.2.11. 波动率(Yang 和 Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)- 1个输出
> vol<-volatility(price[ ,1:4],n = 16,calc = "yang.zhang", N =96) > plot.ts(head(vol, 200))
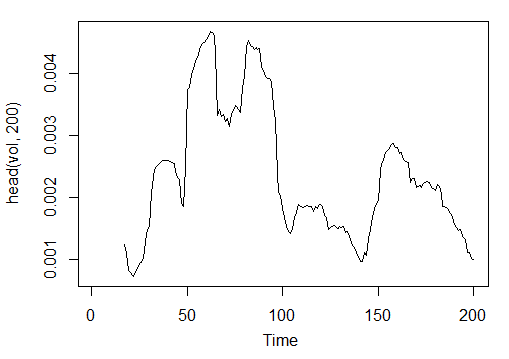
图. 23. 波动率(Yang 和 Zhang)指标 - volatility(OHLC, n, calc="yang.zhang", N=96)
> summary(vol) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 0.000599 0.001858 0.002638 0.003127 0.004015 0.012840 16
至此我们从11个指标中获得了15分钟EURUSD图4000个柱形的OHLC样本的17个变量。
用它们构成一个矩阵并将上面的参数写入有一个正式参数р的函数中,它将用于优化。
使用如下公式计算输入参数矩阵:
In<-function(p = 16){
adx<-ADX(price, n = p);
ar<-aroon(price[ ,c('High', 'Low')], n=p)[ ,'oscillator'];
cci<-CCI(price[ ,2:4], n = p);
chv<-chaikinVolatility(price[ ,2:4], n = p);
cmo<-CMO(price[ ,'Med'], n = p);
macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'];
osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'];
rsi<-RSI(price[ ,'Med'], n = p);
stoh<-stoch(price[ ,2:4],14, 3, 3);
smi<-SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9);
vol<-volatility(price[ ,1:4],n = p,calc="yang.zhang", N=96);
In<-cbind(adx, ar, cci, chv, cmo, macd, osma, rsi, stoh, smi, vol);
return(In)
}
> X<-In()
> tail(X)
DIp DIn DX ADX ar cci chv
[3995,] 46.49620 36.32411 12.28212 18.17544 25.0 168.0407 0.1835102
[3996,] 52.99009 31.61164 25.26952 18.61882 37.5 227.7030 0.3189822
[3997,] 58.11948 28.16241 34.72000 19.62515 37.5 145.2337 0.3448520
[3998,] 56.00323 30.48687 29.50206 20.24245 37.5 118.5831 0.3068059
[3999,] 55.96197 28.78737 32.06467 20.98134 37.5 116.5376 0.3517668
[4000,] 54.97777 26.85440 34.36713 21.81795 62.5 160.0767 0.6169701
cmo macd osma rsi fastK
[3995,] 29.71342 -0.020870825 0.01666593 52.91932 0.8832685
[3996,] 41.89526 -0.009654368 0.02230591 61.49793 0.8833819
[3997,] 30.98237 -0.002051532 0.02392699 58.94513 0.7259475
[3998,] 33.84813 0.003454534 0.02354645 58.00549 0.7930029
[3999,] 38.84892 0.009590136 0.02374564 60.63806 0.8367347
[4000,] 54.71698 0.019303110 0.02676689 66.64815 0.9354120
fastD slowD SMI signal vol
[3995,] 0.7773581 0.7735064 -35.095406 -47.27712 0.003643196
[3996,] 0.7691688 0.7761507 -26.482951 -43.11828 0.003858942
[3997,] 0.8308660 0.7924643 -19.699762 -38.43458 0.003920541
[3998,] 0.8007775 0.8002707 -13.141932 -33.37605 0.003916109
[3999,] 0.7852284 0.8056239 -6.569699 -28.01478 0.003999789
[4000,] 0.8550499 0.8136852 2.197810 -21.97226 0.004293766
准备原始输入数据。
3.3.3. 输出数据(目标)
现在我们可以形成输出了(目标数据)。如前所述,我们将使用ZigZag。
我们将使用通道宽度为37的ZigZag。使用平均价格来计算ZigZag。可以用HL价格来计算该指标,但是使用平均价格能够使得在这种情况下指标更加稳定。解析信号(0 - 买, 1 - 卖),将其转换为网络模型的输入矩阵。
写一个函数:
Out<-function(ch=0.0037){
# ZigZag has values on each bar and not only in the points
zz<-ZigZag(price[ ,'Med'], change = ch, percent = F, retrace = F, lastExtreme = T);
n<-1:length(zz);
# On the last bars substitute the undefined values for the last known ones
for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1];}
#Define the speed of ZigZag changes and move one bar forward
dz<-c(diff(zz), NA);
#If the speed >0 - signal = 0(Buy), if <0, signal = 1 (Sell) otherwise NA
sig<-ifelse(dz>0, 0, if else(dz<0, 1, NA));
return(sig);
}
计算信号。
> Y<-Out() > table(Y) Y 0 1 1567 2423
类型比例失衡。一个类型的数量大于另外一个。所有分类模型在此数据集上都不太理想。
当将数据分为训练和测试样本时,我们将修正这种情况。
3.3.4. 清除数据
从未定义数据中清理我们的数据集。这种情况下的清理意味着宽泛的工作。包括清理“虚拟零值”、强相关的值以及其他一些任务,我们在此不进行讨论。
写一个函数来清理数据
Clearing<-function(x, y){
dt<-cbind(x,y);
n<-ncol(dt)
dt<-na.omit(dt)
return(dt);
}
> dt<-Clearing(X,Y); nrow(dt)
[1] 3957
矩阵缩减了43个柱形。
3.3.5. 训练和测试样本的形成
有很多种方法能将源数据分割为训练和测试样本。我们打算应用常规随机分隔法将原始数据按照8:10的比例,分成训练集和测试集。样本是分层的这一点非常重要,这意味着训练和测试样本中的分类实例的比例必须和原始数据集中的比例一致。在源数据集中修正分类的不均衡也将使后续运算收益。有两个方法来做到这一点 — 调整较大或较小的类别。 因为我们需要更多的样本,我们将调整较大的类别“1”。在这里我们将使用“caret”工具包。
让我们创建一个均衡的数据集,其中两个分类的实例数量一样并且等于较大者。
3.3.6. 分类平衡
下面是调整较大一边分类数量的函数(如果差异大于15%),并返回一个均衡后的矩阵。
Balancing<-function(DT){
#Calculate a table with a number of classes
cl<-table(DT[ ,ncol(DT)]);
#If the divergence is less than 15%, return the initial matrix
if(max(cl)/min(cl)<= 1.15) return(DT)
#Otherwise level by the greater side
DT<-if(max(cl)/min(cl)> 1.15){
upSample(x = DT[ ,-ncol(DT)],y = as.factor(DT[ , ncol(DT)]), yname = "Y")
}
#Convert у (factor) into a number
DT$Y<-as.numeric(DT$Y)
#Recode у from 1,2 into 0,1
DT$Y<-ifelse(DT$Y == 1, 0, 1)
#Convert dataframe to matrix
DT<-as.matrix(DT)
return(DT);
}
解释。首先计算每个分类的实例数量(向量,维度和分类数量相等)。
查找较大向量和较小向量的比例,如果小于预设的阈值,退出。如果比例大于预设的阈值,则计算函数,分别传入x和y。Y必须预先转换为一个因子。
这是upSample() 函数形参的要求。既然我们不需要目标变量作为一个因子,我们将其转换回数值型变量0和1。请注意,当我们将数值型变量(0,1)转换为一个因子时,我们将接收文本变量“0”和“1”。在反向转换为数值变量时,我们得到1和2 (!)。我们用0和1替代。数据集从“数据帧”转换为类型“矩阵”。计算之:
dt.b<-Balancing(dt) x<-dt.b[ ,-ncol(dt.b)] y<-dt.b[ , ncol(dt.b)]
这样我们获得源dt数据集(输入和输出)以及均衡后的数据集dt.b。
将其分割为训练样本和测试样本
使用"rminer"包中的holdout()函数获取训练和测试样本的索引。
> library('rminer')
> t<-holdout(y, ratio = 8/10, mode = "random")
对象t是训练 (t$tr)和测试 (t$ts) 数据集的索引列表。获取到的数据集是分层的。
3.3.7. 预处理
我们的输入源数据变量的值所在范围不同。实质上,深度学习神经网络是具有一种特殊的权值初始化方式的常规网络。
神经网络能够接收输入变量值的范围在(-1; 1) 或 (0, 1)。将输入变量规范化到[-1, 1]之间。
使用"caret"包中的preProcess()函数来实现。请注意预处理的参数是在训练数据集上计算而得的,并将它们保存起来用于对测试数据集以及新的输入数据的处理。
> spSign<-preProcess(x[t$tr, ], method = "spatialSign") > x.tr<-predict(spSign, x[t$tr, ]) > x.ts<-predict(spSign, x[t$ts, ])
至此我们构建、训练以及测试一个深度神经网络的所有要素都已具备。
3.4. 构建,训练和测试模型
我们将构建并训练DN SAE模型。模型公式及变量描述:
sae.dnn.train(x, y, hidden = c(10), activationfun = "sigm", learningrate = 0.8, momentum = 0.5, learningrate_scale = 1, output = "sigm", sae_output = "linear", numepochs = 3, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)
此处:
- х是输入数据矩阵;
- y 是目标变量的一个向量或者矩阵;
- hidden 是一个各隐含层神经元数量的向量。默认 с(10);
- activationfun 是一个激活隐含神经元的函数。可以是 "sigm", "linear", "tanh"。默认为 "sigm";
- learningrate 是梯度下降的训练级数。默认 = 0.8;
- momentum 是一个梯度下降动量。默认 = 0.5;
- learningrate_scale 训练级别在每次迭代后乘以此值。默认 =1.0;
- numepochs 是训练迭代次数。默认 =3;
- batchsize 是被训练的少量数据的规模。默认 =100;
- output 是输出神经元激活函数,可以是"sigm", "linear", "softmax"。默认为 "sigm";
- sae_output 是SAE输出神经元的激活函数,可以是"sigm", "linear", "softmax"。默认为 "linear";
- hidden_dropout 是隐含层可删除部分。默认 =0;
- visible_dropout 是可见(输入)层可删除部分。默认 =0。
我们打算创建一个模型,维度为(17,100,100,100,1)并训练之,注意训练时间并观察其预测结果。
> system.time(SAE<-sae.dnn.train(x= x.tr, y= y[t$tr], hidden=c(100,100,100), activationfun = "tanh", learningrate = 0.6, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 10, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)) 开始训练 sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae 训练完毕。 开始训练深度神经网络 ...... 深度神经网络训练完毕。 user system elapsed 12.92 0.00 13.09
我们可以看到其分两步进行。首先自动编码器逐层训练然后是神经网络。
训练次数少三层隐含神经元数量多是有意这样设置的。整个过程耗时13秒!
让我们来评估预测因子测试集的预测效果。
> pr.sae<-nn.predict(SAE, x.ts); > summary(pr.sae) V1 Min. :0.2649 1st Qu.:0.2649 Median :0.5881 Mean :0.5116 3rd Qu.:0.7410 Max. :0.7410
转换为 0,1 并计算测量值
> pr<-ifelse(pr.sae>mean(pr.sae), 1, 0) > confusionMatrix(y[t$ts], pr) 模糊矩阵统计 Reference Prediction 0 1 0 316 128 1 134 378 Accuracy : 0.7259 95% CI : (0.6965, 0.754) No Information Rate : 0.5293 P-Value [Acc > NIR] : <2e-16 Kappa : 0.4496 Mcnemar's Test P-Value : 0.7574 Sensitivity : 0.7022 Specificity : 0.7470 Pos Pred Value : 0.7117 Neg Pred Value : 0.7383 Prevalence : 0.4707 Detection Rate : 0.3305 Detection Prevalence : 0.4644 Balanced Accuracy : 0.7246 'Positive' Class : 0
这并不是一个出色的相关系数。我们更感兴趣的是使用这些信号能赚多少利润,而不是相关系数。在最近500个柱形(约一周)上检验。我们将在最近的500个连续bar上接收已训练网络的信号。
规范化最近500个柱形的输入数据, 从训练后的神经网络上接收预测信号,将其转换为: -1= (Sell) 和 1 = (Buy)
> new.x<-predict(spSign,tail(dt[ ,-ncol(dt)], 500)) > pr.sae1<-nn.predict(SAE, new.x) > pr.sig<-ifelse(pr.sae1>mean(pr.sae1), -1, 1) > table(pr.sig) pr.sig -1 1 235 265 > new.y<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) > table(new.y) new.y -1 1 201 299 > cm1<-confusionMatrix(new.y, pr.sig) > cm1 模糊矩阵统计 Reference Prediction -1 1 -1 160 41 1 75 224 Accuracy : 0.768 95% CI : (0.7285, 0.8043) No Information Rate : 0.53 P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.5305 Mcnemar's Test P-Value : 0.002184 Sensitivity : 0.6809 Specificity : 0.8453 Pos Pred Value : 0.7960 Neg Pred Value : 0.7492 Prevalence : 0.4700 Detection Rate : 0.3200 Detection Prevalence : 0.4020 Balanced Accuracy : 0.7631 'Positive' Class : -1
精度系数不算差,然而我们更关心获利情况而非系数。
用我们的预测信号测试最近500个柱形上的交易利润情况,并获得资金曲线:
> bal<-cumsum(tail(price[ , 'CO'], 500) * pr.sig) > plot(bal, t = "l") > abline(h = 0)
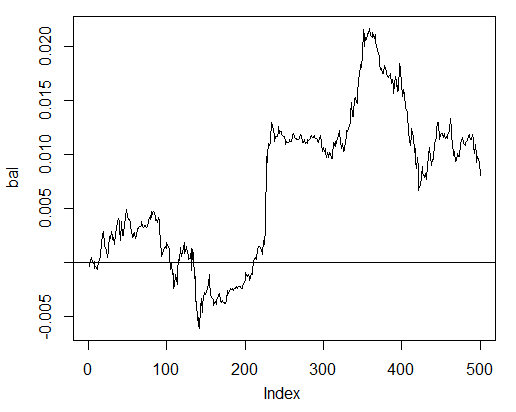
图 24. 根据神经网络信号交易的最近500根柱形上的资金曲线
资金曲线的计算没有考虑点差,滑点以及其他真实市场的相关特性。
现在同理想ZZ信号的资金曲线进行比较。红线是神经网络信号的资金曲线:
> bal.zz<-cumsum(tail(price[ , 'CO'], 500) * new.y) > plot(bal.zz, t = "l") > lines(bal, col = 2)
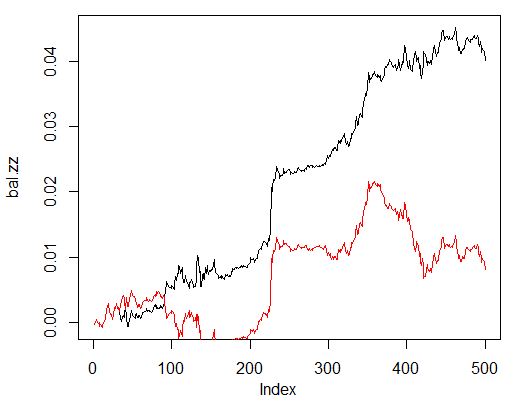
图. 25. 神经网络信号在最近500个柱形上的资金曲线和ZigZag信号
还有改进的余地。
写两个辅助函数Estimation()和Testing()。第一个生成Accuracy/Err系数,第二个生成Bal/BalZZ资金曲线。
它允许直接改变网络参数来获取结果并观察什么参数对网络质量产生影响。
最优网络参数可以通过遗传算法找到二不会对交易过程产生影响。在本文中我们不会花时间研究这个,将在其他时候详细讨论之。
下面是函数Estimation(),用于计算Err/Accuracy系数:
Estimation<-function(X, Y, r = 8/10, m = "random", norm = "spatialSign",
h = c(10), act = "tanh", LR = 0.8, Mom = 0.5,
out = "sigm", sae = "linear", Ep = 10, Bs = 50,
CM=F){
#Indices of the training and test data set
t<-holdout(Y, ratio = r, mode = m)
#Parameters of preprocessing
prepr<-preProcess(X[t$tr, ], method = norm)
#Divide into train and test data sets with preprocessing
x.tr<-predict(prepr, X[t$tr, ])
x.ts<-predict(prepr, X[t$ts, ])
y.tr<- Y[t$tr]; y.ts<- Y[t$ts]
#Train the model
SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h,
activationfun = act,
learningrate = LR, momentum = Mom,
output = out, sae_output = sae,
numepochs = Ep, batchsize = Bs)
#Obtain a forecast on the test data set
pr.sae<-nn.predict(SAE, x.ts)
#Recode it into signals 1,0 pr<-ifelse(pr.sae>mean(pr.sae), 1, 0)
#Calculate the Accuracy coefficient or classification error
if(CM) err<-unname(confusionMatrix(y.ts, pr)$overall[1])
if(!CM) err<-nn.test(SAE, x.ts, y.ts, mean(pr.sae))
return(err)
}
正式参数:
- X – 输入原始预测因子矩阵;
- Y – 目标变量向量;
- r – train/test比例;
- m – 采样模式(随机或连续);
- norm – 输入参数规范化模式 ([ -1, 1]= "spatialSign";[0, 1]="range");
- h – 隐含层神经元向量;
- act – 隐含神经元激活函数;
- LR – 训练级数;
- Мом — 动量;
- out – 输出层激活函数;
- sae – 自动编码器激活函数;
- Ep – 训练周期数量;
- Bs – 小样本尺寸;
- СM– 布尔型变量,如果TRUE打印 Accuracy。否则打印 Err。
作为一个例子,我们将使用共三个隐含层每层含有30个神经元的网络来计算不均衡数据集dt的分类误差:
> Err<-Estimation(X = dt[ ,-ncol(dt)], Y = dt[ ,ncol(dt)], h=c(30, 30, 30), LR= 0.7) 开始训练 sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae 训练完毕。 开始训练深度神经网络 ...... 深度神经网络训练完毕。 > Err [1] 0.1376263
Testing() 函数通过预测信号或者理想信号(ZigZag)来计算资金曲线:
Testing<-function(dt1, dt2, r=8/10, m = "random", norm = "spatialSign",
h = c(10), act = "tanh", LR = 0.8, Mom = 0.5,
out = "sigm", sae = "linear", Ep = 10, Bs=50,
pr = T, bar = 500){
X<-dt1[ ,-ncol(dt1)]
Y<-dt1[ ,ncol(dt1)]
t<-holdout(Y, ratio = r, mode = m)
prepr<-preProcess(X[t$tr, ], method = norm)
x.tr<-predict(prepr, X[t$tr, ])
y.tr<- Y[t$tr];
SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h,
activationfun = act,
learningrate = LR, momentum = Mom,
output = out, sae_output = sae,
numepochs = Ep, batchsize = Bs)
X<-dt2[ ,-ncol(dt2)]
Y<-dt2[ ,ncol(dt2)]
x.ts<-predict(prepr, tail(X, bar))
y.ts<-tail(Y, bar)
pr.sae<-nn.predict(SAE, x.ts)
sig<-ifelse(pr.sae>mean(pr.sae), -1, 1)
sig.zz<-ifelse(y.ts == 0, 1,-1 )
bal<-cumsum(tail(price[ ,'CO'], bar) * sig)
bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz)
if(pr) return(bal)
if(!pr) return(bal.zz)
}
正式参数:
- dt1 – 用于训练网络的输入矩阵和目标变量;
- dt2 - 用于测试网络的输入矩阵和目标变量;
- pr – Boolean 变量, 如果为TRUE根据预测信号交易打印资金曲线,否则根据ZigZag指标交易打印资金曲线;
- bar - 用于计算资金曲线的柱形数量。
当用上述相同参数的神经网络在均衡数据集dt.b 上训练时,计算最近500个柱形数据集dt上的资金曲线:
> Bal<-Testing(dt.b, dt, h=c(30, 30, 30), LR= 0.7) 开始训练 sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae 训练完毕。 开始训练深度神经网络 ...... 深度神经网络训练完毕。 > plot(Bal, t = "l") > abline(h = 0)
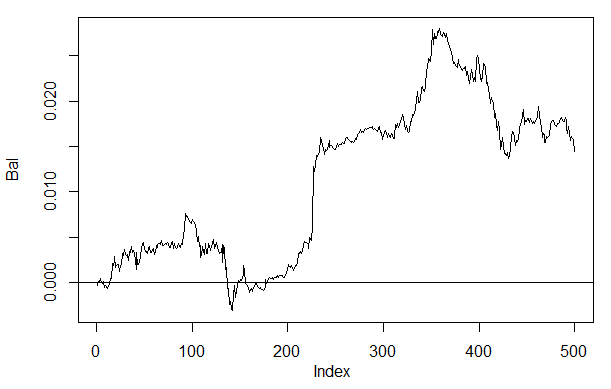
图. 26. 根据神经网络h(30,30,30)信号交易的最近500个柱形上的资金曲线
如果和之前获得的资金曲线做比较,我们会发现有很大的改进。然而这还不是最令人感兴趣的地方。
如果我们观察下最近500个柱形上绘制的价格 ,则能看出我们的神经网络最佳适配的部分(150-350 bars)。
> plot(tail(price[ ,'Close'], 500), t = "l") > abline(v = c(150,350), col=2)
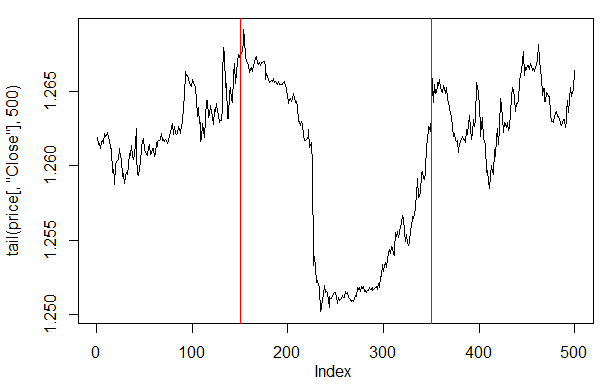
图. 27. 在最近的500个柱形上绘制收盘价格
注意:当译码输出预测值,我们使用大于/小于平均值的简单方案,当然也可以用其他方案。
如果值大于0.6或者小于0.4,则0.4-0.6之间的不稳定部分值将被去除。更为精确的分类边界可以效验后获得。这将在后面进行讨论。
我们将Testing() 函数略微变动下,引入一个额外的参数dec。这样我们就可以选择一种解码方法("mean" or "60/40")并检查预测值看其对资金曲线的影响几何。
Testing.1<-function(dt1, dt2, r = 8/10, m = "random", norm = "spatialSign",
h = c(10), act = "tanh", LR = 0.8, Mom = 0.5,
out = "sigm", sae = "linear", Ep = 10, Bs = 50,
pr = T, bar = 500, dec=1){
X<-dt1[ ,-ncol(dt1)]
Y<-dt1[ ,ncol(dt1)]
t<-holdout(Y, ratio = r, mode = m)
prepr<-preProcess(X[t$tr, ], method = norm)
x.tr<-predict(prepr, X[t$tr, ])
y.tr<- Y[t$tr];
SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h,
activationfun = act,
learningrate = LR, momentum = Mom,
output = out, sae_output = sae,
numepochs = Ep, batchsize = Bs)
X<-dt2[ ,-ncol(dt2)]
Y<-dt2[ ,ncol(dt2)]
x.ts<-predict(prepr, tail(X, bar))
y.ts<-tail(Y, bar)
pr.sae<-nn.predict(SAE, x.ts)
#Вариант +/- mean
if(dec == 1) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1)
#Вариант 60/40 if(dec == 2) sig<-ifelse(pr.sae>0.6, -1, ifelse(pr.sae<0.4, 1, 0))
sig.zz<-ifelse(y.ts == 0, 1,-1 )
bal<-cumsum(tail(price[ ,'CO'], bar) * sig)
bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz)
if(pr) return(bal)
if(!pr) return(bal.zz)
}
使用第一种和第二种解码方式计算及评估资金曲线。
为了能够重现结果,在同一位置上设定伪随机数发生器。
> set.seed<-1245 > Bal1<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 1) 开始训练 sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae 训练完毕。 开始训练深度神经网络 ...... 深度神经网络训练完毕。 > set.seed<-1245 > Bal2<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2) 开始训练 sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae 训练完毕。 开始训练深度神经网络 ...... 深度神经网络训练完毕。 > plot(Bal2, t = "l") > lines(Bal1, col = 2)
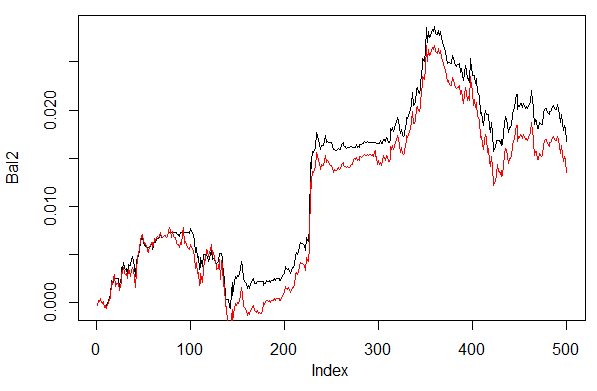
图. 28. 使用不同的方法对神经网络信号进行解码后的最近500根柱形上的资金曲线。
显然,60/40解码方法得到的资金曲线要更好。这方面也还有改进的空间。
这是最后需要检查的地方。理论上,多个神经网络的组合能够获得更好更稳定的结果。我们将测试多个神经网络的组合,将它们在同样的样本上进行训练,虽然也可以在独立的样本上进行训练。组合网络的预测结果是所有神经网络预测的简单平均。还有其他更为复杂的平均方式。
我们打算改进函数Testing(),添加一个参数 — ans=1,定义为组合中网络的数量。
3.4.1. 并行计算
因为多个独立模型的运算可以很容易进行并行处理,我们打算使用R语言提供的机会,创建一个包括多个处理器内核的集群或者与操作系统无关的本地计算机网络。
为了实现这个,我们需要使用"foreach" 和"doParallel"工具包。下面是一个简单的函数,它能够加载计算机集群的所有处理器内核。
library(doParallel) library(foreach)
puskCluster<-function(){
cores<-detectCores()
cl<-makePSOCKcluster(cores)
registerDoParallel(cl)
clusterSetRNGStream(cl) return(cl)
}
下面有几点要解释一下。头两行代码加载必要的类库。它们要预先安装到你的计算机中。然后我们确定处理器中有多少个内核,创建一个集群,注册一个用于并行计算的包,在每个计算线程中注册一个独立的伪随机数发生器并返回集群句柄。每个模型用于运算的伪随机数发生器的质量是非常重要的,然而这是一个单独的话题了。
计算集群加载并所有需要的运算完成后,我们必须记得关闭它:
cl<-puskCluster() stopCluster(cl)
并行运算通过"foreach" 的以下公式进行:
SAE<-foreach(times(ans), .packages = "deepnet") %dopar% sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs)
times(ans)是我们想要获取的网络编号,.packages指向获取计算函数的包。
结果为一个列表形式并且含有我们所需的已经过训练的神经网络数量。
然后我们从每个网络中获取预测值并计算均值。
pr.sae<-(foreach(i = 1:ans, .combine = "+") %do% nn.predict(SAE[[i]], x.ts))/ans
这里i是已训练网络向量的索引,combine="+" 确定所有神经网络中应该返回的预测值形式。在这里,我们要求返回和值并且顺序执行这些运算,而不是并行计算(操作符 %do%)。获得的求和结果将除以神经网络个数,这就是最终的结果。这很好也很简单。
计算具有同上述相同参数的,由3个和4个神经网络组合的资金曲线,并用60/40的方式解码。同一个神经网络的结果进行对比。要评估并行计算的效果,将周期增加到300并且计算预测的时间。
1. 一个神经网络:
> system.time(Bal21<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300)) 开始训练 sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000057 ####loss on step 20000 is : 0.000043 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000081 ####loss on step 20000 is : 0.000086 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000072 ####loss on step 20000 is : 0.000066 sae 训练完毕。 开始训练深度神经网络 ...... ####loss on step 10000 is : 0.069451 ####loss on step 20000 is : 0.079629 深度神经网络训练完毕。 user system elapsed 115.78 0.00 116.96 > plot(Bal21, t = "l") > abline(h = 0)
2. 3个神经网络的组合:
> system.time(Bal41<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=3)) user system elapsed 0.22 0.06 233.64 > lines(Bal41, col=4)
3. 4个神经网络组合:
> system.time(Bal44<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=4)) user system elapsed 0.13 0.03 247.86 > lines(Bal44, col=2)
如果线程的数量是处理器内核数量的倍数,则并行计算的执行时间最快。我使用的是2核处理器。
至于资金取现,没有明显的差异。在下图中,蓝色为3个网络的 - 红色是4个网络以及黑色 - 1个网络。
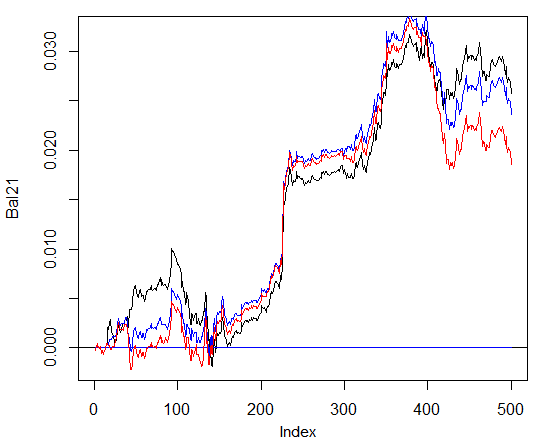
图. 29. 根据3个、4个以及1个网络情况下产生的信号交易后在最近500个柱形上的资金曲线
总的来说,结果取决于很多因素,从输入输出数据开始,规范化它们的方式,隐含层数量以及这些层中的神经元个数,训练级数,训练周期数量等诸多方面。
最后三个例子。用各三个隐含层,每层神经元数量不等的三个神经网络作为信号生成器,计算最近1000个柱形上的资金曲线。
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300, bar=1000)) 开始训练 sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000054 ####loss on step 20000 is : 0.000044 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000078 ####loss on step 20000 is : 0.000079 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000090 ####loss on step 20000 is : 0.000072 sae 训练完毕。 开始训练深度神经网络 ...... ####loss on step 10000 is : 0.072633 ####loss on step 20000 is : 0.057917 深度神经网络训练完毕。 user system elapsed 116.09 0.02 116.26 > max(Bal0) [1] 0.04725 > plot(Bal0, t="l") > tail(Bal0,1) [1] 0.03514
最大利润是472 点,到最近一个柱形截止是351点。图上黑色表示。
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(13, 8, 5), LR = 0.7, dec = 2, Ep=300, bar=1000)) 开始训练 sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.005217 ####loss on step 20000 is : 0.004846 training layer 2 autoencoder ... ####loss on step 10000 is : 0.051324 ####loss on step 20000 is : 0.046230 training layer 3 autoencoder ... ####loss on step 10000 is : 0.023292 ####loss on step 20000 is : 0.026113 sae 训练完毕。 开始训练深度神经网络 ...... ####loss on step 10000 is : 0.057788 ####loss on step 20000 is : 0.056932 深度神经网络训练完毕。 user system elapsed 64.04 0.01 64.24 报警信息: In sae$encoder[[i - 1]]$W[[1]] %*% t(train_x) + sae$encoder[[i - : longer object length is not a multiple of shorter object length > lines(Bal0, col="blue")
显然这是无效的。
第三种:
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=1000)) 开始训练 sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000018 ####loss on step 20000 is : 0.000013 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000062 ####loss on step 20000 is : 0.000048 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000053 ####loss on step 20000 is : 0.000055 sae 训练完毕。 开始训练深度神经网络 ...... ####loss on step 10000 is : 0.096490 ####loss on step 20000 is : 0.084860 深度神经网络训练完毕。 user system elapsed 186.18 0.00 186.39 > lines(Bal0, col="red") > max(Bal0) [1] 0.0543
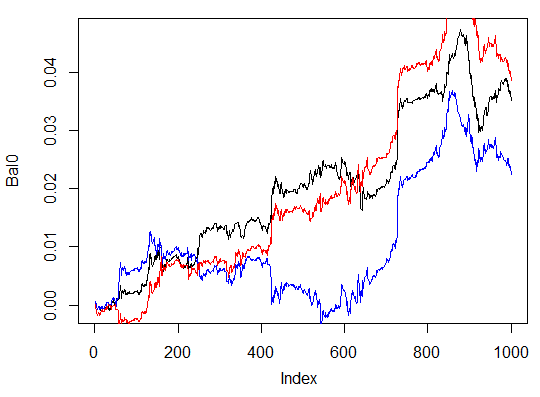
图. 30. 用隐含神经元数量不同的三个神经网络作为信号生成器,计算最近1000个柱形上的资金曲线。
结果显示,第三种是其中效果最好的,最大利润达543点。我们仅仅改变了隐含神经元数量就使得效果大为改观。寻找最优参数得用遗传算法。这就留给读者自己研究了。
读者要记住的是,本文作者的算法并未在这个包中完全实现。
4. 实现(指标和EA)
现在我们要写一个接收深度神经网络交易信号的指标和EA程序。
有两种实现方式:
- 第一种方式。神经网络的训练在Rstudio中手动执行。在获得可接受的结果后,将网络保存在恰当的目录中。然后在图表上加载EA和指标。EA将加载已训练后的神经网络。指标将每个新柱形上的输入数据组织成向量传入EA。EA呈现神经网络数据,接收交易信号然后执行交易。EA执行常规操作如开仓、平仓,追踪止损等。指标的目的是给EA准备和传递每个新柱形的输入数据,最重要的是,在图表上呈现网络的预测信号。实践证明,可视化控制是评估一个神经网络的最有效的方法。
- 第二种方式。在图表上加载EA和指标。刚加载时,指标传递给EA一个预先准备好的输入输出大数据集。EA开始训练、测试及选择最佳神经网络。这之后的运作和第一种方式一样。
我们打算根据第一个算法编写指标-EA关联程序。最简单化实现EA。
为何这么困难呢?这样的实现方式允许将在不同的货币对/时间框架上的多个指标和同一个EA关联起来并正常运行。为了实现这点,EA必须进行小的调整。我们打算后面再讨论它。
下面是指标和EA的交互结构:
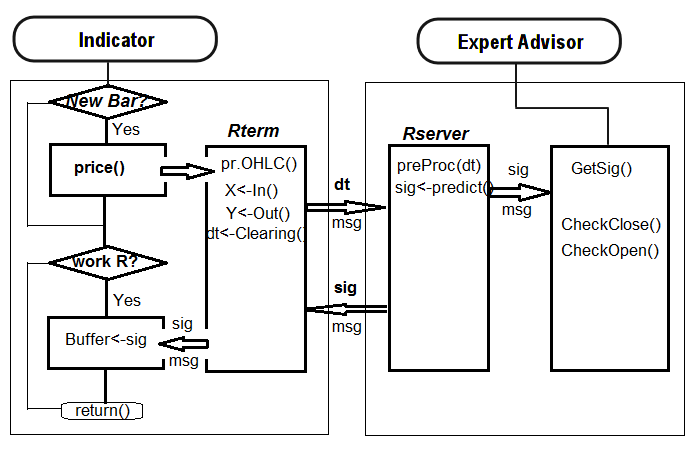
图. 31. 指标和EA之间的交互结构
4.1. 训练和保存模型
将指标加载在我们感兴趣的图表上,获取必要的源数据。将指标放到图表上,例如,将输入参数send设置为false,可视化展现不被发送到服务端。在首次加载到货币对或时间框架上后,指标将在终端(/MQL4/Files)的数据文件夹下创建如下目录:/Symbol/TF/Test_Data/。
这样的目录组织方式将能够将实验结果和预先训练好的网络模型区别放置,并且新的数据不会将旧数据覆盖。中间结果将被保存在/Symbol/TF/Test_Data/目录下,并且EA将要使用的网络模型位于/Symbol/TF/目录下(必须手动将其放到这里)。首次加载在一个新的货币对图表或者EA所在的时间框架上,将获得同样的结果。
因此,对于EURUSD,М30,在 14.10.2014 有4000个柱形。我们使用dt[]时间框架。
资金类:
> dt.b<-Balancing(dt) > table(dt.b[ ,ncol(dt.b)]) 0 1 2288 2288
现在用之前编写的Testing.1()函数训练500和300个周期的深度神经网络,并且根据神经网络预测的信号进行交易,获得最近500个柱形上的资金曲线。
> system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=500, bar=500)) 开始训练 sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000017 ####loss on step 20000 is : 0.000015 ####loss on step 30000 is : 0.000015 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000044 ####loss on step 20000 is : 0.000041 ####loss on step 30000 is : 0.000039 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000042 ####loss on step 20000 is : 0.000042 ####loss on step 30000 is : 0.000036 sae 训练完毕。 开始训练深度神经网络 ...... ####loss on step 10000 is : 0.089417 ####loss on step 20000 is : 0.043276 ####loss on step 30000 is : 0.069399 深度神经网络训练完毕。 user system elapsed 267.59 0.08 269.37 > plot(bal, t="l")
将此神经网络换个名字保存下来并训练另一个网络。
> SAE1<-SAE > system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=500)) 开始训练 sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000020 ####loss on step 20000 is : 0.000016 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000050 ####loss on step 20000 is : 0.000050 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000051 ####loss on step 20000 is : 0.000043 sae 训练完毕。 开始训练深度神经网络 ...... ####loss on step 10000 is : 0.083888 ####loss on step 20000 is : 0.083941 深度神经网络训练完毕。 user system elapsed 155.32 0.02 156.25 > lines(bal, col=2)
看一下资金曲线图(最新结果用红色表示)。
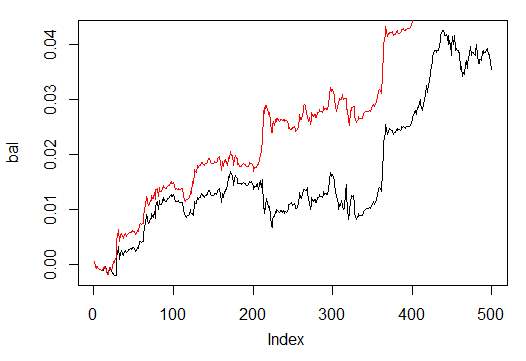
图. 32. 根据训练了500和300周期的神经网络信号交易的最近500个柱形上的资金曲线
如我们所见,经过300个周期训练的神经网络所呈现的结果要好于500个的。
如要在此时间框架上、在一个训练会话内快速的再学习,后者的训练时间更为合适。
我们需要两个对象在真实图表上进行进一步操作:已训练模型"SAE"以及用于输入的规范化参数"prepr"。将它们保存在相关目录中,在我这里是"D:/Alpari Limited MT4/MQL4/Files/EURUSD/M30/Test_2014-10-14"。如果你在Rstdio中打开由指标所保存的"i_SAE_EURUSD_30.Rdata"工作区,这就是已经定义和操作所用的数据。
save(SAE, prepr, file="SAE.model")
在 "SAE.model"文件中我们保存了模型本身及规范化后的参数。不使用它们的模型没有意义。你可以每天测试和保存你喜欢的模型。它们将被保存在文件夹"/File/Symbol/TF/Test_Data"下。对于使用模型的EA,将"SAE.model"文件手动放到文件夹"File/Symbol/TF/"下。这个文件夹只能保留一个模型,EA将使用这个模型来工作。
加载完"SAE.model"文件,EA将这些对象加载到工作区用于运行。至此人工操作部分的工作结束了,你可以将指标-EA加载到图表上实际测试了。
要获知EA的有效性就需要量化的衡量标准。准确度系数作为衡量标准此时就不是非常稳定了。
由ZigZag获取到的资金预测平均值比例和最近柱形的资金和柱形数量的比例。这是根据ZigZag指标得到的资金余额:
sig.zz<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) bal.zz<-cumsum(tail(price[ , 'CO'], 500) * sig.zz) Kzz<-mean(bal.zz / bal) > Kzz [1] 0.9173312
这是个结果非常好,但只是相对的。
如果我们随着时间推移来看看它,我们会发现最初的50-100个柱形上并不稳定,但是后来逐渐接近常数。统计如下:
> plot(bal/bal.zz, t="l") > summary(bal/bal.zz) Min. 1st Qu. Median Mean 3rd Qu. Max. -15.2500 0.7341 0.7844 0.9173 0.8833 55.0000
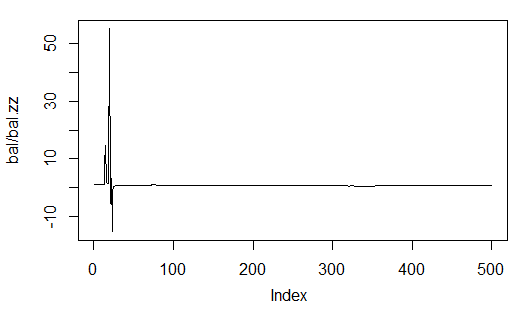
图. 33. 神经网络预测交易和由ZigZag指标交易所得的资金余额比
第二个更加精确,因为它显示了再长度为N的柱形区间上每个bar上获得的利润点数。
例如,由神经网络预测交易的500个柱形上的资金余额:
> Kb<-tail(bal,1)/length(bal)*10^Dig > Kb [1] 11.508
ZigZag信号交易:
> Kbz<-tail(bal.zz,1)/length(bal)*10^Dig > Kbz [1] 13.784
当一个参数的有效下限被定义,我们就可以重新训练神经网络或者优化其参数。
EA将在图表上显示下述参数:OP - 执行操作,Acc - 准确率,K - 是之前定义的Kb,Kmax - 同Kb一样,但是由资金高点定义,给出这个参数的最大值和最近柱形上的值的差异。
4.2. 安装和加载命令
在附件SAE.zip中有:
- i_SAE.mq4 指标,放在 ~/MQL4/Indicators/ 目录下。
- e_SAE.mq4 EA,放在 ~/MQL4/Experts/ 目录下。
- mt4Rb7.dll 库,放在 ~/MQL4/Libraries/ 目录下。
- mt4Rb7.mqh 头文件,放在 ~/MQL4/Include/ 目录下。库和头文件由Bernd Kreuss开发。文件名称包含了最新更新版本的索引号(b7)。当有众多同名版本时会让人感到困惑,要花很多时间来理清。
- R的脚本:i_SAE.r(主要指标脚本),i_SAE_fun.r(指标脚本函数),e_SAE.r(EA脚本),e_SAE_init.r(EA初始化脚本), SAE_SetDir.r(用于验证的脚本以及创建目录的脚本)。脚本既不依赖于货币对也不依赖时间框架,它们能够存放在一个独立的目录中。我是放在 "C:Rdata/SAE/" 下。"C:Rdata/" 目录包含不同的脚本,它们不附属于任何一个项目。如果你的脚本所在目录和我的不一样,那么亲保证在指标和EA中修改使得其能够正确的调用脚本。
- SAE.model 是含有"SAE"模型及规范化参数"prepr"的文件。模型在EURUSD (M30)上训练所得,最新的行情时间是 14.10.2014。训练过程上面已经阐释。
也别忘了R语言程序包在你计算机中的存储位置。
最好依照下面的步骤开始。将EA加载到图表上。如果你决定将EA加载到另外一个货币对上,需要确定一个和之前加载的服务器不同的端口。例如,端口8886(默认端口8888)。
注意。这显然不是高效的方式。每个服务器空间约120-130 Mb。这就是如今的情形。
在EA初始化后,告警“没有计算结果!货币对" 将出现。然后安装带有外部参数send = true的指标并确定指标要连接的服务器端口(见上面)。如果所有的工作都正确无误,真实数据“operation”,Accuracy,K 和 Kmax将在输出字符串中出现并且将开始执行交易。
此处理过程最有效的管理方式就是通过Windows任务管理器了。当EA或者指标加载后,如果Rterm没有在任务列表中出现,那么说明R处理器崩溃了。这个问题的主要原因是脚本中的一个语法错误,接收到的MQL向量长度和从Rterm中解析的向量长度不匹配导致的。
这个问题可以通过在Rstudio中将脚本从头至尾逐行debug来修复。
不幸的是我没能够在策略测试器中加载这个EA,因为它必须用模拟账户进行测试。
4.3. 改进质量特征的途径和方法
- 改变用作输入的指标集。
- 改变输入数据规范化的方式。
- 优化“监督者”和指标的输入参数。
- 为具有两列的矩阵改变输入变量的编码。校准预测信号。
- 优化网络参数(隐含层的神经元数量,层数,学习级数,周期数)。
总结
我们已经创建、训练并测试了深度神经网络模型,在隐含层通过SAE初始化了神经元权值。重新训练网络速度非常快,并且无需打断交易过程。
神经网络显示的结果是统计平均值。一个理想的结果并不是最初的目标。
使用这样的模型和有效性系数的持续评估,该模型和优化而不破坏交易过程。

